Trasformata di segnali periodici

Treno di impulsi

Prima di esaurire l'elencazione delle proprietà della trasformata di Fourier, presentiamo un diverso modo di ottenere lo spettro di un segnale periodico, facendo uso della particolare forma d'onda (ideale)

$\pi_{T}^{}$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = $\sum^{\infty }_{m=-\infty }$$\delta$$\left(\vphantom{ t-mT}\right.$t - mT$\left.\vphantom{ t-mT}\right)$

chiamata treno di impulsi, e che si rivelerà di utilizzo frequente nei contesti del campionamento e delle trasmissioni numeriche.

Segnale periodico

Consideriamo un segnale periodico di periodo T espresso come

x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = $\sum^{\infty }_{m=-\infty }$g$\left(\vphantom{ t-mT}\right.$t - mT$\left.\vphantom{ t-mT}\right)$

di cui g$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ costituisce un periodo: la riproduzione di infinite repliche di g$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$, spaziate di un periodo T l'una dall'altra, ricompongono il segnale periodico originario. Sfruttando la proprietà di convoluzione con l'impulso traslato, la stessa somma può essere scritta come

x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = $\sum^{\infty }_{m=-\infty }$g$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$*$\delta$$\left(\vphantom{ t-mT}\right.$t - mT$\left.\vphantom{ t-mT}\right)$ = g$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$*$\sum^{\infty }_{m=-\infty }$$\delta$$\left(\vphantom{ t-mT}\right.$t - mT$\left.\vphantom{ t-mT}\right)$ = g$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$*$\pi_{T}^{}$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$

dove nel secondo passaggio si è sfruttata la linearità della convoluzione. Ricordando ora la proprietà della moltiplicazione in frequenza, troviamo X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = G$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ ^. $\mathcal {F}$$\left\{\vphantom{ \pi _{T}\left( t\right) }\right.$$\pi_{T}^{}$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ $\left.\vphantom{ \pi _{T}\left( t\right) }\right\}$; ci accingiamo allora a determinare $\mathcal {F}$$\left\{\vphantom{ \pi _{T}\left( t\right) }\right.$$\pi_{T}^{}$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ $\left.\vphantom{ \pi _{T}\left( t\right) }\right\}$, 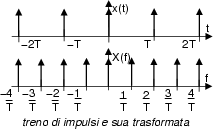ossia la trasformata del treno di impulsi.

Trasformata del treno di impulsi

 

0.350000

L'approccio che conviene seguire è di pensare a $\pi_{T}^{}$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ come ad un segnale periodico, e svilupparlo in serie di Fourier. I coefficienti si calcolano allora come:

$\Pi_{n}^{}$	=	${\frac{1}{T}}$ $\int_{-\frac{T}{2}}^{\frac{T}{2}}$$\left[\vphantom{ \sum ^{\infty }_{m=-\infty }\delta \left( t-mT\right) }\right.$$\sum^{\infty }_{m=-\infty }$$\delta$$\left(\vphantom{ t-mT}\right.$t - mT$\left.\vphantom{ t-mT}\right)$ $\left.\vphantom{ \sum ^{\infty }_{m=-\infty }\delta \left( t-mT\right) }\right]$ e-j2$\pi$nFtdt
	=	${\frac{1}{T}}$ $\int_{-\frac{T}{2}}^{\frac{T}{2}}$$\delta$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ e-j2$\pi$nFtdt = ${\frac{1}{T}}$ $\int_{-\frac{T}{2}}^{\frac{T}{2}}$1 . $\delta$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ dt = ${\frac{1}{T}}$

in quanto, tra tutti gli impulsi della sommatoria, ne resta solo uno, quello centrato in zero, dato che gli altri sono tutti esterni ai limiti di integrazione; pertanto, tutti i coefficienti risultano avere lo stesso valore, pari ad ${\frac{1}{T}}$, e possiamo dunque scrivere

$\mathcal {F}$$\left\{\vphantom{ \pi _{T}\left( t\right) }\right.$$\pi_{T}^{}$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ $\left.\vphantom{ \pi _{T}\left( t\right) }\right\}$ = $\mathcal {F}$$\left\{\vphantom{ \sum ^{\infty }_{n=-\infty }\Pi _{n}\hbox {e}^{j2\pi nFt}}\right.$$\sum^{\infty }_{n=-\infty }$$\Pi_{n}^{}$e^j2$\pi$nFt$\left.\vphantom{ \sum ^{\infty }_{n=-\infty }\Pi _{n}\hbox {e}^{j2\pi nFt}}\right\}$ = ${\frac{1}{T}}$$\sum^{\infty }_{n=-\infty }$$\delta$$\left(\vphantom{ f-\frac{n}{T}}\right.$f - ${\frac{n}{T}}$ $\left.\vphantom{ f-\frac{n}{T}}\right)$ = ${\frac{1}{T}}$$\pi_{\frac{1}{T}}^{}$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$

ottenendo il risultato cercato: $\mathcal {F}$$\left\{\vphantom{ \pi _{T}\left( t\right) }\right.$$\pi_{T}^{}$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ $\left.\vphantom{ \pi _{T}\left( t\right) }\right\}$ = ${\frac{1}{T}}$$\pi_{\frac{1}{T}}^{}$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$. Pertanto, la trasformata di un treno di impulsi è a sua volta un treno di impulsi, di periodo inverso a quello originario.

Trasformata di segnale periodico

Siamo finalmente in grado di esprimere la trasformata di un segnale periodico come il prodotto tra la $\mathcal {F}$-trasformata di un suo periodo ed un treno di impulsi in frequenza:

X$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ = G$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ ^. $${\frac{1}{T}}$$$$\pi_{\frac{1}{T}}^{}$$$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$

Esempio

Riprendendo in considerazione il caso dell'onda quadra affrontato in 2.2.1.2, non è difficile riconoscere come, ponendo g$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = Arect_$\tau$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$, e corrispondentemente G$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = A$\tau$sinc$\left(\vphantom{ f\tau }\right.$f$\tau$ $\left.\vphantom{ f\tau }\right)$, il prodotto di G$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ per il treno di impulsi ${\frac{1}{T}}$$\sum^{\infty }_{n=-\infty }$$\delta$$\left(\vphantom{ f-nF}\right.$f - nF$\left.\vphantom{ f-nF}\right)$ (con F = ${\frac{1}{T}}$) fornisce il risultato già incontrato: X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = A${\frac{\tau }{T}}$$\sum^{\infty }_{n=-\infty }$sinc$\left(\vphantom{ nF\tau }\right.$nF$\tau$ $\left.\vphantom{ nF\tau }\right)$$\delta$$\left(\vphantom{ f-nF}\right.$f - nF$\left.\vphantom{ f-nF}\right)$.