Derivazione ed Integrazione nel Tempo

Le ultime due proprietà riguardano un risultato di applicazione meno frequente, ma talvolta utile. Si ottiene infatti che le operazioni di derivata ed integrale di un segnale possono essere realizzate mediante il passaggio dello stesso attraverso un sistema fisico, in quanto tali operazioni nel tempo sono equivalenti a dei prodotti in frequenza, realizzabili in forma di convoluzione del segnale per una risposta impulsiva.

Derivazione nel Tempo

E' equivalente a moltiplicare lo spettro per j2$\pi$f:

$$\mathcal {F}$$$$\left\{\vphantom{ \frac{d}{dt}x\left( t\right) }\right.$$$${\frac{d}{dt}}$$x$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ $$\left.\vphantom{ \frac{d}{dt}x\left( t\right) }\right\}$$ = j2$$\pi$$f ^. X$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$

e più in generale $\mathcal {F}$$\left\{\vphantom{ \frac{d^{n}}{dt^{n}}x\left( t\right) }\right.$${\frac{d^{n}}{dt^{n}}}$x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ $\left.\vphantom{ \frac{d^{n}}{dt^{n}}x\left( t\right) }\right\}$ = $\left(\vphantom{ j2\pi f}\right.$j2$\pi$f$\left.\vphantom{ j2\pi f}\right)^{n}_{}$ ^. X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$. Per segnali di energia, la dimostrazione è svolta nella nota^3.12.

L'andamento dello spettro originario X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ risulta esaltato alle frequenze più elevate, in quanto il suo modulo è moltiplicato per 2$\pi$$\left\vert\vphantom{ f}\right.$f$\left.\vphantom{ f}\right\vert$, dato che $\left\vert\vphantom{ Z\left( f\right) }\right.$Z$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ $\left.\vphantom{ Z\left( f\right) }\right\vert$ = $\left\vert\vphantom{ 2\pi f}\right.$2$\pi$f$\left.\vphantom{ 2\pi f}\right\vert$ ^. $\left\vert\vphantom{ X\left( f\right) }\right.$X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ $\left.\vphantom{ X\left( f\right) }\right\vert$. La fase, invece, subisce un incremento di ${\frac{\pi }{2}}$ a tutte le frequenze (il numero immaginario puro j2$\pi$f = 2$\pi$f e^{j${\frac{\pi }{2}}$} ha fase ${\frac{\pi }{2}}$).

Esempio

Calcolare Y$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = $\mathcal {F}$$\left\{\vphantom{ y\left( t\right) }\right.$y$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ $\left.\vphantom{ y\left( t\right) }\right\}$ con y$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = ${\frac{d}{dt}}$x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ e x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = cos 2$\pi$f₁t + cos 2$\pi$f₂t. Valutare quindi y$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = $\mathcal {F}$^-1$\left\{\vphantom{ Y\left( f\right) }\right.$Y$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ $\left.\vphantom{ Y\left( f\right) }\right\}$ con f₁ = 10, f₂ = 100.

Si ottiene: X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = ${\frac{1}{2}}$$\left(\vphantom{ \delta \left( f-f_{1}\right) +\delta \left( f+f_{1}\right) +\delta \left( f-f_{2}\right) +\delta \left( f+f_{2}\right) }\right.$$\delta$$\left(\vphantom{ f-f_{1}}\right.$f - f₁$\left.\vphantom{ f-f_{1}}\right)$ + $\delta$$\left(\vphantom{ f+f_{1}}\right.$f + f₁$\left.\vphantom{ f+f_{1}}\right)$ + $\delta$$\left(\vphantom{ f-f_{2}}\right.$f - f₂$\left.\vphantom{ f-f_{2}}\right)$ + $\delta$$\left(\vphantom{ f+f_{2}}\right.$f + f₂$\left.\vphantom{ f+f_{2}}\right)$ $\left.\vphantom{ \delta \left( f-f_{1}\right) +\delta \left( f+f_{1}\right) +\delta \left( f-f_{2}\right) +\delta \left( f+f_{2}\right) }\right)$. Dato che

f ^. $\delta$$\left(\vphantom{ f-a}\right.$f - a$\left.\vphantom{ f-a}\right)$ = a ^. $\delta$$\left(\vphantom{ f-a}\right.$f - a$\left.\vphantom{ f-a}\right)$, risulta:

Y$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = j2$\pi$${\frac{1}{2}}$$\left[\vphantom{ f_{1}\left( \delta \left( f-f_{1}\right) -\delta \left( f+f_{... ...ft( \delta \left( f-f_{2}\right) -\delta \left( f+f_{2}\right) \right) }\right.$f₁$\left(\vphantom{ \delta \left( f-f_{1}\right) -\delta \left( f+f_{1}\right) }\right.$$\delta$$\left(\vphantom{ f-f_{1}}\right.$f - f₁$\left.\vphantom{ f-f_{1}}\right)$ - $\delta$$\left(\vphantom{ f+f_{1}}\right.$f + f₁$\left.\vphantom{ f+f_{1}}\right)$ $\left.\vphantom{ \delta \left( f-f_{1}\right) -\delta \left( f+f_{1}\right) }\right)$ + f₂$\left(\vphantom{ \delta \left( f-f_{2}\right) -\delta \left( f+f_{2}\right) }\right.$$\delta$$\left(\vphantom{ f-f_{2}}\right.$f - f₂$\left.\vphantom{ f-f_{2}}\right)$ - $\delta$$\left(\vphantom{ f+f_{2}}\right.$f + f₂$\left.\vphantom{ f+f_{2}}\right)$ $\left.\vphantom{ \delta \left( f-f_{2}\right) -\delta \left( f+f_{2}\right) }\right)$ $\left.\vphantom{ f_{1}\left( \delta \left( f-f_{1}\right) -\delta \left( f+f_{... ...ft( \delta \left( f-f_{2}\right) -\delta \left( f+f_{2}\right) \right) }\right]$

Considerando ora che j2$\pi$${\frac{1}{2}}$ = - ${\frac{2\pi }{2j}}$, si ottiene y$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = - 2$\pi$f₁sin$\omega_{1}^{}$t - 2$\pi$f₂sin$\omega_{2}^{}$t e quindi, per f₁ = 10 e f₂ = 100, si ha

y$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = - 2$\pi$$\left[\vphantom{ 10\sin \omega _{1}t+100\sin \omega _{2}t}\right.$10sin$\omega_{1}^{}$t + 100sin$\omega_{2}^{}$t$\left.\vphantom{ 10\sin \omega _{1}t+100\sin \omega _{2}t}\right]$

Integrazione nel Tempo

E' equivalente a dividere lo spettro per j2$\pi$f:

$$\mathcal {F}$$$$\left\{\vphantom{ \int ^{t}_{-\infty }x\left( \theta \right) d\theta }\right.$$$$\int^{t}_{-\infty }$$x$$\left(\vphantom{ \theta }\right.$$$$\theta$$ $$\left.\vphantom{ \theta }\right)$$d$$\theta$$ $$\left.\vphantom{ \int ^{t}_{-\infty }x\left( \theta \right) d\theta }\right\}$$ = $${\frac{X\left( f\right) }{j2\pi f}}$$

Tale risultato è diretta conseguenza del precedente, in virtù dei legami tra integrale e derivata. Infatti, $\int^{t}_{-\infty }$x$\left(\vphantom{ \theta }\right.$$\theta$ $\left.\vphantom{ \theta }\right)$d$\theta$ è una funzione di t, che compare nel limite superiore di integrazione, e la sua derivata è proprio x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$.

In questo caso, le basse frequenze del segnale originario sono esaltate seguendo un andamento 1/2$\pi$$\left\vert\vphantom{ f}\right.$f$\left.\vphantom{ f}\right\vert$, mentre la fase subisce una variazione (un ritardo) costante pari a - ${\frac{\pi }{2}}$. Notiamo come questo risultato determini una singolarità per f = 0 in presenza di componenti continue per x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$: in tal caso infatti il suo integrale tende a divergere e non è più di energia.

Esempio: Trasformata di un triangolo

 

0.300000

Consideriamo un segnale

x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = rect_T$\left(\vphantom{ t+\frac{T}{2}}\right.$t + ${\frac{T}{2}}$ $\left.\vphantom{ t+\frac{T}{2}}\right)$ - rect_T$\left(\vphantom{ t-\frac{T}{2}}\right.$t - ${\frac{T}{2}}$ $\left.\vphantom{ t-\frac{T}{2}}\right)$

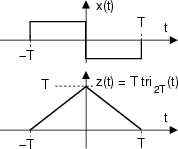
ed il suo integrale

z$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = $\int^{t}_{-\infty }$x$\left(\vphantom{ \theta }\right.$$\theta$ $\left.\vphantom{ \theta }\right)$d$\theta$ = T tri_2T$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$

entrambi rappresentati in figura: z$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ è nullo fino a t < - T, cresce linearmente fino a t = 0, e quindi il contributo all'integrale dato dall'area del rect negativo torna ad annullarne il valore.

Per calcolare la $\mathcal {F}$-trasformata di z$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$, calcoliamo prima quella di x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$, e poi applichiamo la proprietà dell'integrazione. Applicando la proprietà di traslazione nel tempo, scriviamo

X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$	=	Tsinc$\left(\vphantom{ fT}\right.$fT$\left.\vphantom{ fT}\right)$e+j2$\pi$f${\frac{T}{2}}$ - Tsinc$\left(\vphantom{ fT}\right.$fT$\left.\vphantom{ fT}\right)$e-j2$\pi$f${\frac{T}{2}}$ = T${\frac{\sin \left( \pi fT\right) }{\pi fT}}$2jsin$\pi$fT
	=	j2T${\frac{\sin ^{2}\left( \pi fT\right) }{\pi fT}}$

Dividendo quindi per j2$\pi$f si ottiene

Z$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = ${\frac{j2T}{j2\pi f}}$${\frac{\sin ^{2}\left( \pi fT\right) }{\pi fT}}$${\frac{T}{T}}$ = $\left(\vphantom{ T\frac{\sin \left( \pi fT\right) }{\pi fT}}\right.$T${\frac{\sin \left( \pi fT\right) }{\pi fT}}$ $\left.\vphantom{ T\frac{\sin \left( \pi fT\right) }{\pi fT}}\right)^{2}_{}$ = $\left(\vphantom{ T\hbox {sinc}\left ( fT\right ) }\right.$Tsinc$\left(\vphantom{ fT}\right.$fT$\left.\vphantom{ fT}\right)$ $\left.\vphantom{ T\hbox {sinc}\left ( fT\right ) }\right)^{2}_{}$

il cui andamento è mostrato in figura 3.4

Figura: Andamento di $\left(\vphantom{ T\hbox {sinc}\left ( fT\right ) }\right.$Tsinc$\left(\vphantom{ fT}\right.$fT$\left.\vphantom{ fT}\right)$ $\left.\vphantom{ T\hbox {sinc}\left ( fT\right ) }\right)^{2}_{}$in scala lineare e logaritmica; T = 10.

.

Lo stesso risultato può essere ottenuto per altra via, notando che

z$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ = tri_2T$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ = rect_T$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$*rect_T$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$

Come verifica, si ripercorra la costruzione grafica riportata alla sezione 3.6. Basta quindi applicare la proprietà del prodotto nel tempo, per ottenere:

Z$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ = $$\left[\vphantom{ \mathcal{F}\left\{ rect_{T}\left( t\right) \right\} }\right.$$$$\mathcal {F}$$$$\left\{\vphantom{ rect_{T}\left( t\right) }\right.$$rect_T$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ $$\left.\vphantom{ rect_{T}\left( t\right) }\right\}$$ $$\left.\vphantom{ \mathcal{F}\left\{ rect_{T}\left( t\right) \right\} }\right]^{2}_{}$$ = $$\left[\vphantom{ Tsinc\left( fT\right) }\right.$$Tsinc$$\left(\vphantom{ fT}\right.$$fT$$\left.\vphantom{ fT}\right)$$ $$\left.\vphantom{ Tsinc\left( fT\right) }\right]^{2}_{}$$

L'esempio ci dà inoltre modo di notare che, essendo Y$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = Tsinc$\left(\vphantom{ fT}\right.$fT$\left.\vphantom{ fT}\right)$ la trasformata di y$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = rect_T$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$, allora $\left[\vphantom{ Tsinc\left( fT\right) }\right.$Tsinc$\left(\vphantom{ fT}\right.$fT$\left.\vphantom{ fT}\right)$ $\left.\vphantom{ Tsinc\left( fT\right) }\right]^{2}_{}$ = $\mathcal {E}$_y$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ è lo spettro di densità di energia di un segnale rettangolare.