




Avanti: Derivazione ed Integrazione nel Tempo
Su: Trasformata di Fourier
Indietro: Convoluzione con l'impulso traslato
Indice
Indice analitico
La descrizione di un sistema fisico per mezzo della sua risposta impulsiva è
di fondamentale utilità soprattutto per merito della seguente proprietà della
trasformata di Fourier:
La
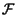 -trasformata della convoluzione tra
due segnali è pari al prodotto delle trasformate dei segnali:
-trasformata della convoluzione tra
due segnali è pari al prodotto delle trasformate dei segnali:
La dimostrazione è riportata alla nota3.10. Sussiste inoltre anche la proprietà duale, ovvero ad un un prodotto
nel tempo corrispponde una convoluzione in frequenza , che si scrive
Trattiamo ora delle conseguenze e dei risvolti legati a queste due importanti
proprietà, iniziando dalla prima.
L'applicazione più importante è legata al calcolo dell'uscita da un sistema
fisico: questo può essere interamente condotto nel dominio della frequenza,
calcolando
e quindi ottenendo
y t
t =
= 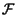 -1
-1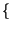 Y
Y f
f
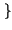 .
La trasformata della risposta impulsiva
H
.
La trasformata della risposta impulsiva
H f
f =
= 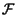
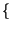 h
h t
t
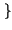 prende allora il nome di risposta in frequenza, in quanto rappresenta
l'alterazione introdotta dal sistema per ogni frequenza presente in
X
prende allora il nome di risposta in frequenza, in quanto rappresenta
l'alterazione introdotta dal sistema per ogni frequenza presente in
X f
f .
Facciamo ora un paio di esempi per sperimentare questo modo di procedere.
.
Facciamo ora un paio di esempi per sperimentare questo modo di procedere.
- Sistema passa tutto
- Poniamo di avere
H
 f
f = 1, e che quindi
risulti
h
= 1, e che quindi
risulti
h t
t =
= 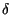
 t
t . In questo caso le
componenti di
X
. In questo caso le
componenti di
X f
f alle diverse frequenze non subiscono
nessuna alterazione, ottenendo
y
alle diverse frequenze non subiscono
nessuna alterazione, ottenendo
y t
t =
= 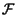 -1
-1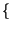 Y
Y f
f
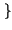 =
= 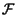 -1
-1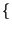 X
X f
f
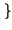 = x
= x t
t ,
ed il sistema viene detto di tipo passa tutto. Per verifica, scriviamo
l'integrale di convoluzione, che risulta
y
,
ed il sistema viene detto di tipo passa tutto. Per verifica, scriviamo
l'integrale di convoluzione, che risulta
y t
t =
= 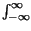 x
x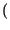

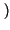
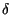
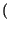 t -
t - 
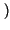 d
d = x
= x t
t :
ritroviamo quindi la proprietà di setacciamento.
:
ritroviamo quindi la proprietà di setacciamento.
- Ritardo
- Se invece
H
 f
f = e-j2
= e-j2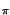 f
f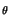 , pari
cioè ad un esponenziale complesso, il sistema equivale ad una linea di ritardo,
riproducendo in uscita l'ingresso presentatosi
, pari
cioè ad un esponenziale complesso, il sistema equivale ad una linea di ritardo,
riproducendo in uscita l'ingresso presentatosi  istanti prima.
Infatti risulta:
y
istanti prima.
Infatti risulta:
y t
t =
= 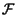 -1
-1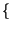 Y
Y f
f
 =
= 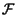 -1
-1 X
X f
f e-j2
e-j2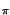 f
f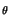
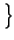 = x
= x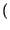 t -
t - 
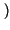 .
D'altra parte, scrivendo l'integrale di convoluzione, e ricordando che
h
.
D'altra parte, scrivendo l'integrale di convoluzione, e ricordando che
h t
t =
= 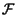 -1
-1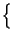 e-j2
e-j2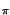 f
f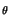
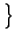 =
= 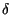
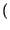 t -
t - 
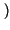 ,
avremmo ottenuto
y
,
avremmo ottenuto
y t
t =
= 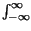 x
x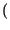

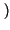
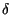
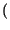 t -
t -  -
- 
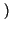 d
d = x
= x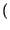 t -
t - 
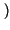 ,
ritrovando la proprietà della convoluzione per un impulso traslato.
,
ritrovando la proprietà della convoluzione per un impulso traslato.
La relazione
ci permette di investigare le conseguenze frequenziali del prodotto temporale
di due segnali.
A titolo di esempio, analizziamo il caso in cui
z t
t = ArectT
= ArectT t
t cos 2
cos 2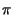 f0t,
la cui forma d'onda è graficata a sinistra della Fig. 3.3
f0t,
la cui forma d'onda è graficata a sinistra della Fig. 3.3
Figura:
Trasformata di un coseno finestrato con
T = 2,
f0 = 10
|
. Applicando i risultati noti e la proprietà di traslazione in frequenza, risulta:
Z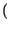 f f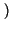 |
= |
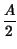 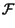 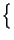 rectT rectT t t 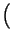 ej2 ej2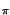 f0t + e-j2 f0t + e-j2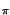 f0t f0t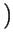 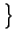 |
| |
= |
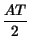 ![$\displaystyle \left[\vphantom{ \hbox {sinc}\left[ \left( f-f_{0}\right) T\right] +\hbox {sinc}\left[ \left( f+f_{0}\right) T\right] }\right.$](img687.gif) sinc sinc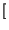 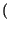 f - f0 f - f0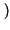 T T![$\displaystyle \left.\vphantom{ \left( f-f_{0}\right) T}\right]$](img689.gif) + sinc + sinc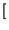 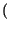 f + f0 f + f0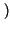 T T![$\displaystyle \left.\vphantom{ \left( f+f_{0}\right) T}\right]$](img691.gif) ![$\displaystyle \left.\vphantom{ \hbox {sinc}\left[ \left( f-f_{0}\right) T\right] +\hbox {sinc}\left[ \left( f+f_{0}\right) T\right] }\right]$](img692.gif) |
in cui la
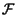
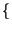 rectT
rectT t
t
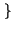 = Tsinc
= Tsinc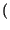 fT
fT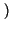 si è traslata in
si è traslata in 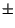 f0. Verifichiamo che il risultato coincida con
quanto previsto: l'espressione di
Z
f0. Verifichiamo che il risultato coincida con
quanto previsto: l'espressione di
Z f
f infatti è anche pari
alla convoluzione tra
infatti è anche pari
alla convoluzione tra
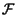
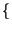 rectT
rectT t
t
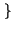 ed i due impulsi traslati
ed i due impulsi traslati
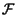
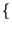 cos 2
cos 2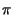 f0t
f0t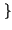 =
= 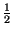
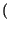
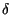
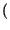 f - f0
f - f0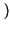 -
- 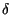
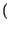 f + f0
f + f0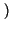
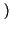 .
.
Osserviamo ora che quanto maggiore è l'estensione T
della finestra3.11 di segnale cosinusoidale, tanto più il risultato tende ad essere simile a quello
per una cosinusoide ``infinita''. Infatti, qualora si consideri solamente
un breve intervallo di un segnale, il suo spettro si modifica a seguito
della sua convoluzione con lo spettro della finestra di analisi.
L'esempio proposto ci permette inoltre di motivare il termine Modulazione
associato a questa proprietà. L'ampiezza del coseno risulta infatti modulata
dal rettangolo. La modulazione di ampiezza (AM) dei radio ricevitori
casalinghi si riferisce esattamente a questo processo, svolto allo scopo di
condividere tra più emittenti la banda prevista per le trasmissioni, assegnando
a ciascuna di esse una diversa frequenza portante f0 su cui trasmettere.
Sottosezioni





Avanti: Derivazione ed Integrazione nel Tempo
Su: Trasformata di Fourier
Indietro: Convoluzione con l'impulso traslato
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
-trasformata della convoluzione tra due segnali è pari al prodotto delle trasformate dei segnali:
![]() t
t![]() = ArectT
= ArectT![]() t
t![]() cos 2
cos 2![]() f0t,
la cui forma d'onda è graficata a sinistra della Fig. 3.3
f0t,
la cui forma d'onda è graficata a sinistra della Fig. 3.3
![]()
![]() rectT
rectT![]() t
t![]()
![]() = Tsinc
= Tsinc![]() fT
fT![]() si è traslata in
si è traslata in ![]() f0. Verifichiamo che il risultato coincida con
quanto previsto: l'espressione di
Z
f0. Verifichiamo che il risultato coincida con
quanto previsto: l'espressione di
Z![]() f
f![]() infatti è anche pari
alla convoluzione tra
infatti è anche pari
alla convoluzione tra
![]()
![]() rectT
rectT![]() t
t![]()
![]() ed i due impulsi traslati
ed i due impulsi traslati
![]()
![]() cos 2
cos 2![]() f0t
f0t![]() =
= ![]()
![]()
![]()
![]() f - f0
f - f0![]() -
- ![]()
![]() f + f0
f + f0![]()
![]() .
.