Teorema del Campionamento

Un segnale con spettro nullo a frequenze maggiori di W, è univocamente definito a partire dai valori che assume agli istanti t = ${\frac{n}{2W}}$.

La frequenza 2W è chiamata frequenza di Nyquist. In virtù del teorema, l'andamento di un segnale x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ limitato in banda tra - W e W può essere ricostruito in base ai suoi campioni, presi a frequenza doppia della sua banda a frequenze positive, per mezzo della formula:

Figura: funzione sinc$\left(\vphantom{ 2Wt}\right.$2Wt$\left.\vphantom{ 2Wt}\right)$ centrata in 0 e traslata in ${\frac{3}{2W}}$

$$\left(\vphantom{ t}\right. \left.\vphantom{ t}\right) \sum^{\infty }_{n=-\infty } \left(\vphantom{ \frac{n}{2W}}\right. {\frac{n}{2W}} \left.\vphantom{ \frac{n}{2W}}\right) \left(\vphantom{ 2W\left( t-\frac{n}{2W}\right) }\right. \left(\vphantom{ t-\frac{n}{2W}}\right. {\frac{n}{2W}} \left.\vphantom{ t-\frac{n}{2W}}\right) \left.\vphantom{ 2W\left( t-\frac{n}{2W}\right) }\right)$$ (4.1)

in cui la funzione sinc$\left(\vphantom{ 2Wt}\right.$2Wt$\left.\vphantom{ 2Wt}\right)$ = ${\frac{\sin 2\pi Wt}{2\pi Wt}}$ è mostrata in Fig. 4.1, assieme ad una sua replica traslata.

Per dimostrare analiticamente il risultato, studiamo innanzitutto il circuito riportato in Fig. 4.2, che mostra uno schema simbolico che (come vedremo) realizza le stesse operazioni della formula di ricostruzione, in cui si operi un campionamento con periodo T_c = ${\frac{1}{2W}}$. Calcoliamo innanzitutto lo spettro di ampiezza X^$\bullet$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ del segnale che esce dal moltiplicatore, che ha subìto un'alterazione notevole rispetto a quello di X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ in ingresso. Infatti, il segnale x^$\bullet$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ ha uno spettro di ampiezza

Figura: di campionamento e restituzione, e spettri dei segnali

      

$$\bullet \left(\vphantom{ f}\right. \left.\vphantom{ f}\right) \mathcal {F} \left\{\vphantom{ x\left( t\right) \cdot \pi _{T_{c}}\left( t\right) }\right. \left(\vphantom{ t}\right. \left.\vphantom{ t}\right) \pi_{T_{c}}^{} \left(\vphantom{ t}\right. \left.\vphantom{ t}\right) \left.\vphantom{ x\left( t\right) \cdot \pi _{T_{c}}\left( t\right) }\right\} \left(\vphantom{ f}\right. \left.\vphantom{ f}\right) {\frac{1}{T_{c}}} \Pi_{\frac{1}{T_{c}}}^{} \left(\vphantom{ f}\right. \left.\vphantom{ f}\right) \left(\vphantom{ f}\right. \left.\vphantom{ f}\right) {\frac{1}{T_{c}}} \sum^{\infty }_{n=-\infty } \delta \left(\vphantom{ f-\frac{n}{T_{c}}}\right. {\frac{n}{T_{c}}} \left.\vphantom{ f-\frac{n}{T_{c}}}\right)$$ =

$$\sum^{\infty }_{n=-\infty } \left(\vphantom{ f}\right. \left.\vphantom{ f}\right) \delta \left(\vphantom{ f-n2W}\right. \left.\vphantom{ f-n2W}\right) \sum^{\infty }_{n=-\infty } \left(\vphantom{ f-n2W}\right. \left.\vphantom{ f-n2W}\right)$$ =

dove il penultimo passaggio scambia l'integrale di una somma con una somma di integrali, e l'ultimo passaggio tiene conto della proprietà di setacciamento dell'impulso. In definitiva si è mostrato che X^$\bullet$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ è costituito dalle repliche di X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ centrate a multipli della frequenza di campionamento. Pertanto, il filtro passa-basso H$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ (chiamato anche con il nome di filtro di restituzione) lascia passare solo una delle repliche spettrali, e dunque è evidente come Y$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = ${\frac{1}{2W}}$2W ^. X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$.

Per quanto riguarda la formula di ricostruzione che fa uso dei campioni x$\left(\vphantom{ \frac{n}{2W}}\right.$${\frac{n}{2W}}$ $\left.\vphantom{ \frac{n}{2W}}\right)$ e delle funzioni sinc$\left(\vphantom{ 2Wt}\right.$2Wt$\left.\vphantom{ 2Wt}\right)$, anch'essa deriva dallo schema illustrato. Infatti y$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ è il risultato della convoluzione tra x^$\bullet$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ e h$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = $\mathcal {F}$^-1$\left\{\vphantom{ H\left( f\right) }\right.$H$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ $\left.\vphantom{ H\left( f\right) }\right\}$ = $\mathcal {F}$^-1$\left\{\vphantom{ \frac{1}{2W}\hbox {rect}_{2W}\left( f\right) }\right.$${\frac{1}{2W}}$rect_2W$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ $\left.\vphantom{ \frac{1}{2W}\hbox {rect}_{2W}\left( f\right) }\right\}$ = sinc$\left(\vphantom{ 2Wt}\right.$2Wt$\left.\vphantom{ 2Wt}\right)$ e dunque ogni impulso di cui è composto x^$\bullet$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$, quando convoluto con h$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$, ne trasla la forma d'onda al proprio istante. In formule:

y$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$	=	$\left[\vphantom{ x\left( t\right) \cdot \sum _{n}\delta \left( t-nT_{c}\right) }\right.$x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ . $\sum_{n}^{}$$\delta$$\left(\vphantom{ t-nT_{c}}\right.$t - nTc$\left.\vphantom{ t-nT_{c}}\right)$ $\left.\vphantom{ x\left( t\right) \cdot \sum _{n}\delta \left( t-nT_{c}\right) }\right]$*h$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$
	=	$\sum_{n}^{}$x$\left(\vphantom{ nT_{c}}\right.$nTc$\left.\vphantom{ nT_{c}}\right)$$\delta$$\left(\vphantom{ t-nT_{c}}\right.$t - nTc$\left.\vphantom{ t-nT_{c}}\right)$*sinc$\left(\vphantom{ 2Wt}\right.$2Wt$\left.\vphantom{ 2Wt}\right)$ =
	=	$\sum_{n}^{}$x$\left(\vphantom{ nT_{c}}\right.$nTc$\left.\vphantom{ nT_{c}}\right)$sinc$\left(\vphantom{ 2W\left( t-nT_{c}\right) }\right.$2W$\left(\vphantom{ t-nT_{c}}\right.$t - nTc$\left.\vphantom{ t-nT_{c}}\right)$ $\left.\vphantom{ 2W\left( t-nT_{c}\right) }\right)$

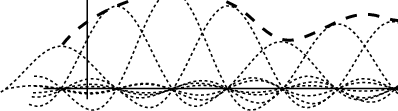
Questo risultato mostra come il teorema del campionamento definisca essenzialmente una formula di interpolazione: i valori del segnale ricostruito hanno l'esatto valore dei campioni di segnale negli istanti di campionamento, mentre negli istanti intermedi il valore si forma dalla somma di tutte le ``code'' dei sinc adiacenti. Il processo di costruzione grafica ora descritto è riportato nella figura precedente.