




Avanti: ProbabilitÓ condizionali
Su: Teoria delle probabilitÓ
Indietro: Assiomi delle probabilitÓ
Indice
Indice analitico
-
Pr
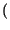
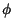
 = 0: la probabilitÓ dell'evento
impossibile Ŕ nulla.
= 0: la probabilitÓ dell'evento
impossibile Ŕ nulla.
-
Pr
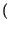 A
A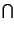 B
B + Pr
+ Pr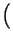 A
A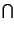
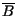
 = Pr
= Pr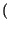 A
A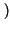 e
Pr
e
Pr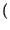 B
B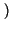 + Pr
+ Pr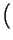
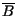
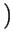 = 1: un evento ed il
suo complemento riempiono lo spazio (noto anche come teorema delle probabilitÓ
totali5.1
)
= 1: un evento ed il
suo complemento riempiono lo spazio (noto anche come teorema delle probabilitÓ
totali5.1
)
-
Pr
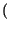 A
A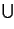 B
B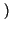 = Pr
= Pr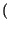 A
A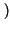 + Pr
+ Pr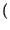 B
B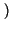 - Pr
- Pr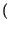 A
A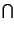 B
B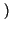 :
la probabilitÓ dell'evento intersezione va contata una sola volta. Ad esempio:
la probabilitÓ
Pr
:
la probabilitÓ dell'evento intersezione va contata una sola volta. Ad esempio:
la probabilitÓ
Pr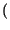 pari
pari 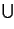 > 2
> 2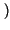 che lanciando un dado
si ottenga un numero pari, oppure pi˙ grande di due, Ŕ la somma delle
probabilitÓ dei singoli eventi
Pr
che lanciando un dado
si ottenga un numero pari, oppure pi˙ grande di due, Ŕ la somma delle
probabilitÓ dei singoli eventi
Pr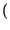 pari
pari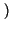 =
= 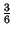 e
Pr
e
Pr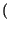 > 2
> 2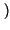 =
= 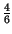 ,
meno la probabilitÓ che si verifichino assieme
Pr
,
meno la probabilitÓ che si verifichino assieme
Pr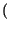 pari
pari 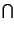 > 2
> 2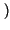 =
= 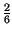 .
Pertanto:
Pr
.
Pertanto:
Pr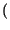 pari
pari 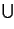 > 2
> 2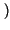 =
= 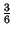 +
+ 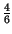 -
- 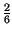 =
= 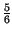 .
.
- Se
B
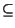 A allora
Pr
A allora
Pr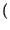 B
B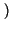
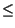 Pr
Pr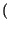 A
A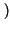 :
quando l'evento B Ŕ contenuto in A il verificarsi del primo implica
il secondo.
:
quando l'evento B Ŕ contenuto in A il verificarsi del primo implica
il secondo.
alef@infocom.uniroma1.it
2001-06-01