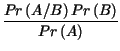Avanti: Teorema di Bayes
Su: Teoria delle probabilitÓ
Indietro: Teoremi di base
Indice
Indice analitico
Pu˛ avvenire che il verificarsi di un evento influenzi il verificarsi
o meno di un altro: Si dice allora che lo condiziona, ovvero che l'evento influenzato
Ŕ condizionato. La probabilitÓ che avvenga A, noto che B
si sia verificato, si scrive
Pr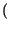 A/B
A/B , e si legge probabilitÓ
(condizionata) di A dato B, che Ŕ definita come
, e si legge probabilitÓ
(condizionata) di A dato B, che Ŕ definita come
in cui
Pr A, B
A, B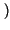 = Pr
= Pr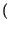 A
A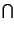 B
B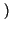 Ŕ la probabilitÓ
congiunta che A e B si verifichino entrambi, ed a patto
che
Pr
Ŕ la probabilitÓ
congiunta che A e B si verifichino entrambi, ed a patto
che
Pr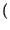 B
B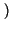
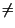 0 (altrimenti anche
Pr
0 (altrimenti anche
Pr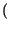 A/B
A/B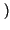 Ŕ zero!).
Ŕ zero!).
- Esempio:
- la probabilitÓ che lanciando un dado si ottenga un numero pari, condizionatamente
all'evento che il numero sia >2, Ŕ pari alla probabilitÓ che i due risultati
si verifichino contemporaneamente, diviso per la probabilitÓ che il numero sia
>2(5.2
).
A partire dalla precedente definizione, si ottiene quella della probabilitÓ
congiunta:
Pr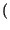 A, B
A, B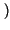 = Pr
= Pr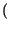 A/B
A/B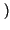 Pr
Pr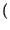 B
B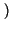 ;
inoltre, gli eventi condizionante e condizionato possono invertire i rispettivi
ruoli, permettendo di scrivere anche:
Pr
;
inoltre, gli eventi condizionante e condizionato possono invertire i rispettivi
ruoli, permettendo di scrivere anche:
Pr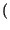 A, B
A, B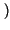 = Pr
= Pr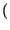 B/A
B/A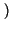 Pr
Pr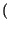 A
A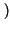 .
Eguagliando le due espressioni, si ottiene:
.
Eguagliando le due espressioni, si ottiene:
Come ultima definizione, rammentiamo che le probabilitÓ
Pr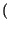 A
A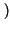 e
Pr
e
Pr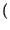 B
B sono indicate come marginali.
sono indicate come marginali.





Avanti: Teorema di Bayes
Su: Teoria delle probabilitÓ
Indietro: Teoremi di base
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() A/B
A/B![]() , e si legge probabilitÓ
(condizionata) di A dato B, che Ŕ definita come
, e si legge probabilitÓ
(condizionata) di A dato B, che Ŕ definita come
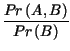
![]() A, B
A, B![]() = Pr
= Pr![]() A/B
A/B![]() Pr
Pr![]() B
B![]() ;
inoltre, gli eventi condizionante e condizionato possono invertire i rispettivi
ruoli, permettendo di scrivere anche:
Pr
;
inoltre, gli eventi condizionante e condizionato possono invertire i rispettivi
ruoli, permettendo di scrivere anche:
Pr![]() A, B
A, B![]() = Pr
= Pr![]() B/A
B/A![]() Pr
Pr![]() A
A![]() .
Eguagliando le due espressioni, si ottiene:
.
Eguagliando le due espressioni, si ottiene:
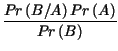 ed anche Pr
ed anche Pr