A volte, non tutti i possibili eventi sono direttamente osservabili: in tal
caso la probabilitÓ marginale
Pr![]() A
A![]() Ŕ indicata come probabilitÓ
a priori. Qualora l'evento A sia in qualche modo legato ad un
secondo evento B, che invece possiamo osservare, la probabilitÓ condizionata
Pr
Ŕ indicata come probabilitÓ
a priori. Qualora l'evento A sia in qualche modo legato ad un
secondo evento B, che invece possiamo osservare, la probabilitÓ condizionata
Pr![]() A/B
A/B![]() prende il nome di probabilitÓ a posteriori
perchÚ, a differenza di quella a priori, rappresenta un valore di probabilitÓ
valutata dopo la conoscenza di B.
prende il nome di probabilitÓ a posteriori
perchÚ, a differenza di quella a priori, rappresenta un valore di probabilitÓ
valutata dopo la conoscenza di B.
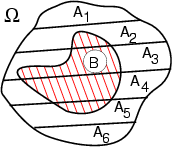
L'ultima relazione ci permette di enunciare il teorema preannunciato, che mostra come ottenere le probabilitÓ a posteriori a partire da quelle a priori e da quelle condizionate in avanti:
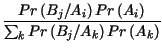
Illustriamo un caso pratico di utilizzo del teorema di Bayes nell'ambito di una sua applicazione ad un problema di telecomunicazioni: la decisione statistica.
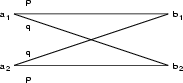
Qualora si osservi in uscita uno dei due valori (ad es. b1), si possono
confrontare le probabilitÓ a posteriori per le due possibili ipotesi
che in ingresso fosse presente a1 od a2 (ad es. valutando
il rapporto
![]() =
= ![]() ),
e quindi decidere per l'ipotesi pi˙ verosimile (es. si decide per a1
se p > q, ovvero se
Pe <
),
e quindi decidere per l'ipotesi pi˙ verosimile (es. si decide per a1
se p > q, ovvero se
Pe < ![]() ).
).
Se disponiamo della conoscenza delle probabilitÓ a priori
Pr![]() a1
a1![]() e
Pr
e
Pr![]() a2
a2![]() , possiamo costruire il rapporto di verosimiglianza
utilizzando le probabilitÓ a posteriori
Pr
, possiamo costruire il rapporto di verosimiglianza
utilizzando le probabilitÓ a posteriori
Pr![]() a1/b1
a1/b1![]() e
Pr
e
Pr![]() a2/b1
a2/b1![]() , calcolabili applicando il teorema di
Bayes. Per fissare le idee, poniamo di aver ricevuto il simbolo b1,
e pertanto il rapporto di verosimiglianza si scrive come
, calcolabili applicando il teorema di
Bayes. Per fissare le idee, poniamo di aver ricevuto il simbolo b1,
e pertanto il rapporto di verosimiglianza si scrive come
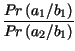
La metodologia ora descritta prende il nome di verifica di ipotesi statistica e si basa appunto sul confronto di quanto la grandezza osservata sia verosimile compatibilmente con le ipotesi possibili. Se RV utilizza solamente le probabilitÓ in avanti, la decisione si dice di massima verosimiglianza (indicata com ML o MAXIMUM LIKELIHOOD), mentre se si impiegano le probabilitÓ a posteriori, si sta effettuando una decisione bayesiana.
Il meccanismo con cui, nella decisione Bayesiana, le probabilitÓ in avanti si
combinano con quelle a priori, pu˛ essere analizzato mediante alcune osservazioni:
innanzi tutto, a1 potrebbe essere cosÝ ``raro'' che, in presenza
di una moderata probabilitÓ di errore, il ricevitore potrebbe preferire di decidere
sempre a2, attribuendo l'eventuale ricezione di b1 dovuta
pi˙ verosimilmente ad un errore piuttosto che all'effettiva partenza di a1.
In assenza di canale inoltre, l'unico rapporto di verosimiglianza possibile
sarebbe stato quello tra le probabilitÓ a priori
Pr![]() a1
a1![]() e
Pr
e
Pr![]() a2
a2![]() ; la ricezione di un simbolo bi dunque
ha portato un miglior livello di informazione, alterando il RV, in misura
tanto maggiore quanto pi˙ bassa Ŕ la probabilitÓ di errore.
; la ricezione di un simbolo bi dunque
ha portato un miglior livello di informazione, alterando il RV, in misura
tanto maggiore quanto pi˙ bassa Ŕ la probabilitÓ di errore.
Verifichiamo i ragionamenti appena svolti riscrivendo per esteso una probabilitÓ a posteriori:
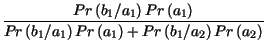 =
= 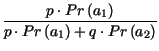
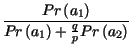 > Pr
> Pr
Infine, nel casi in cui i simboli in ingresso abbiano uguale probabilitÓ
Pr![]() a1
a1![]() = Pr
= Pr![]() a2
a2![]() ,
la decisione Bayesiana Ŕ equivalente a quella di massima verosimiglianza. Infatti:
,
la decisione Bayesiana Ŕ equivalente a quella di massima verosimiglianza. Infatti:
| RV | = | 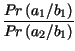 = = 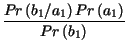 . . 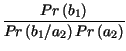 |
|
| = | 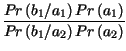 |