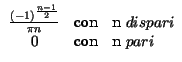Avanti: Teorema di Parseval
Su: Serie di Fourier
Indietro: Serie Trigonometrica
Indice
Indice analitico
Consideriamo un'onda quadra con duty-cycle del 50%
rappresentata mediante una serie troncata di Fourier in cui si considerano solo
i coefficienti Xn con indice
- N 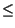 n
n 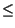 N. Sappiamo che
Xn =
N. Sappiamo che
Xn = 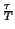
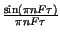 e, per
e, per
 =
= 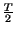 , si ottiene
Xn =
, si ottiene
Xn = 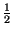
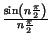 =
= 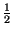 sinc
sinc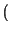
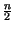
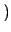 ,
che risulta diverso da zero solo con n dispari, e dunque:
Essendo inoltre
x
,
che risulta diverso da zero solo con n dispari, e dunque:
Essendo inoltre
x t
t reale pari, sappiamo che può essere
espresso come serie di coseni:
x
reale pari, sappiamo che può essere
espresso come serie di coseni:
x t
t = X0 +
= X0 + 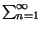 2Xncos
2Xncos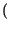 2
2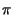 nFt
nFt .
.
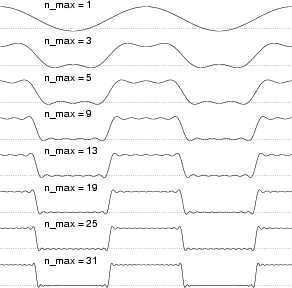
Nella figura a fianco riportiamo il risultato ottenuto arrestando lo sviluppo
in serie all'indice mostrato per ogni curva, e generando quindi il segnale
Come osservabile, la ricostruzione è sempre più accurata, tranne che per le
oscillazioni in prossimità della discontinuità, che prendono il nome di Fenomeno
di Gibbs.
Il caso mostrato è emblematico della inaccuratezza che si commette considerando
contributi frequenziali ridotti rispetto a quelli propri della forma d'onda2.6, a causa (ad esempio) di un filtraggio del segnale.





Avanti: Teorema di Parseval
Su: Serie di Fourier
Indietro: Serie Trigonometrica
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01